I was generating, for an example model, a random, sparse, directed graph. Unfortunately, when sparse enough, this is likely to yield a graph that is not connected. Here is my first attempt.
Nodes
I generate simply \(n=25\) nodes with \((x,y)\) coordinates from a uniform distribution \(U(0,100)\). This looks like:
Node data
---- 29 SET i nodes node1 , node2 , node3 , node4 , node5 , node6 , node7 , node8 , node9 , node10, node11, node12 node13, node14, node15, node16, node17, node18, node19, node20, node21, node22, node23, node24 node25 ---- 29 PARAMETER p node locations (points) x y node1 4.421 38.227 node2 62.306 57.268 node3 46.068 87.792 node4 92.771 59.338 node5 27.269 83.898 node6 76.650 57.983 node7 90.958 77.730 node8 44.593 15.935 node9 39.514 27.723 node10 17.519 49.107 node11 56.134 61.680 node12 75.507 50.566 node13 25.469 81.568 node14 23.978 51.624 node15 87.866 29.493 node16 17.431 41.679 node17 21.801 37.073 node18 93.156 30.535 node19 86.431 31.005 node20 11.040 14.150 node21 35.467 61.779 node22 43.955 11.814 node23 25.659 46.821 node24 32.996 32.370 node25 0.684 65.249 ---- 29 PARAMETER d distances node1 .node2 60.936, node1 .node3 64.739, node1 .node4 90.837, node1 .node5 51.067, node1 .node6 74.882 node1 .node7 95.127, node1 .node8 45.943, node1 .node9 36.631, node1 .node10 17.027, node1 .node11 56.782 node1 .node12 72.149, node1 .node13 48.181, node1 .node14 23.706, node1 .node15 83.901, node1 .node16 13.460 node1 .node17 17.418, node1 .node18 89.068, node1 .node19 82.327, node1 .node20 24.970, node1 .node21 38.969 node1 .node22 47.546, node1 .node23 22.911, node1 .node24 29.169, node1 .node25 27.279, node2 .node1 60.936 node2 .node3 34.575, node2 .node4 30.536, node2 .node5 44.009, node2 .node6 14.362, node2 .node7 35.209 node2 .node8 44.968, node2 .node9 37.315, node2 .node10 45.525, node2 .node11 7.587, node2 .node12 14.804 node2 .node13 44.130, node2 .node14 38.741, node2 .node15 37.746, node2 .node16 47.506, node2 .node17 45.260 node2 .node18 40.821, node2 .node19 35.662, node2 .node20 66.988, node2 .node21 27.216, node2 .node22 49.019 node2 .node23 38.107, node2 .node24 38.457, node2 .node25 62.136, node3 .node1 64.739, node3 .node2 34.575 node3 .node4 54.688, node3 .node5 19.198, node3 .node6 42.707, node3 .node7 46.003, node3 .node8 71.872 node3 .node9 60.426, node3 .node10 48.079, node3 .node11 27.985, node3 .node12 47.459, node3 .node13 21.519 node3 .node14 42.380, node3 .node15 71.735, node3 .node16 54.282, node3 .node17 56.226, node3 .node18 74.133 node3 .node19 69.671, node3 .node20 81.548, node3 .node21 28.090, node3 .node22 76.008, node3 .node23 45.773 node3 .node24 56.943, node3 .node25 50.674, node4 .node1 90.837, node4 .node2 30.536, node4 .node3 54.688 node4 .node5 69.956, node4 .node6 16.178, node4 .node7 18.481, node4 .node8 64.846, node4 .node9 61.935 node4 .node10 75.945, node4 .node11 36.713, node4 .node12 19.365, node4 .node13 70.878, node4 .node14 69.224 node4 .node15 30.246, node4 .node16 77.382, node4 .node17 74.381, node4 .node18 28.805, node4 .node19 29.034 node4 .node20 93.392, node4 .node21 57.356, node4 .node22 68.130, node4 .node23 68.270, node4 .node24 65.577 node4 .node25 92.276, node5 .node1 51.067, node5 .node2 44.009, node5 .node3 19.198, node5 .node4 69.956 node5 .node6 55.768, node5 .node7 63.987, node5 .node8 70.137, node5 .node9 57.494, node5 .node10 36.131 node5 .node11 36.426, node5 .node12 58.634, node5 .node13 2.944, node5 .node14 32.441, node5 .node15 81.437 node5 .node16 43.350, node5 .node17 47.143, node5 .node18 84.787, node5 .node19 79.359, node5 .node20 71.611 node5 .node21 23.589, node5 .node22 73.991, node5 .node23 37.112, node5 .node24 51.845, node5 .node25 32.473 node6 .node1 74.882, node6 .node2 14.362, node6 .node3 42.707, node6 .node4 16.178, node6 .node5 55.768 node6 .node7 24.386, node6 .node8 52.874, node6 .node9 47.904, node6 .node10 59.794, node6 .node11 20.847 node6 .node12 7.504, node6 .node13 56.354, node6 .node14 53.054, node6 .node15 30.618, node6 .node16 61.422 node6 .node17 58.700, node6 .node18 32.029, node6 .node19 28.697, node6 .node20 78.905, node6 .node21 41.358 node6 .node22 56.574, node6 .node23 52.199, node6 .node24 50.613, node6 .node25 76.312, node7 .node1 95.127 node7 .node2 35.209, node7 .node3 46.003, node7 .node4 18.481, node7 .node5 63.987, node7 .node6 24.386 node7 .node8 77.255, node7 .node9 71.744, node7 .node10 78.820, node7 .node11 38.345, node7 .node12 31.251 node7 .node13 65.601, node7 .node14 71.887, node7 .node15 48.337, node7 .node16 81.889, node7 .node17 80.223 node7 .node18 47.246, node7 .node19 46.945, node7 .node20 102.124, node7 .node21 57.738, node7 .node22 80.959 node7 .node23 72.245, node7 .node24 73.601, node7 .node25 91.132, node8 .node1 45.943, node8 .node2 44.968 node8 .node3 71.872, node8 .node4 64.846, node8 .node5 70.137, node8 .node6 52.874, node8 .node7 77.255 node8 .node9 12.836, node8 .node10 42.819, node8 .node11 47.178, node8 .node12 46.422, node8 .node13 68.363 node8 .node14 41.216, node8 .node15 45.347, node8 .node16 37.424, node8 .node17 31.085, node8 .node18 50.710 node8 .node19 44.469, node8 .node20 33.601, node8 .node21 46.744, node8 .node22 4.171, node8 .node23 36.228 node8 .node24 20.115, node8 .node25 66.029, node9 .node1 36.631, node9 .node2 37.315, node9 .node3 60.426 node9 .node4 61.935, node9 .node5 57.494, node9 .node6 47.904, node9 .node7 71.744, node9 .node8 12.836 node9 .node10 30.677, node9 .node11 37.806, node9 .node12 42.630, node9 .node13 55.647, node9 .node14 28.507 node9 .node15 48.384, node9 .node16 26.123, node9 .node17 20.029, node9 .node18 53.716, node9 .node19 47.032 node9 .node20 31.543, node9 .node21 34.296, node9 .node22 16.518, node9 .node23 23.594, node9 .node24 8.004 node9 .node25 53.999, node10.node1 17.027, node10.node2 45.525, node10.node3 48.079, node10.node4 75.945 node10.node5 36.131, node10.node6 59.794, node10.node7 78.820, node10.node8 42.819, node10.node9 30.677 node10.node11 40.610, node10.node12 58.006, node10.node13 33.420, node10.node14 6.933, node10.node15 73.030 node10.node16 7.429, node10.node17 12.773, node10.node18 77.884, node10.node19 71.250, node10.node20 35.552 node10.node21 21.971, node10.node22 45.713, node10.node23 8.455, node10.node24 22.797, node10.node25 23.323 node11.node1 56.782, node11.node2 7.587, node11.node3 27.985, node11.node4 36.713, node11.node5 36.426 node11.node6 20.847, node11.node7 38.345, node11.node8 47.178, node11.node9 37.806, node11.node10 40.610 node11.node12 22.334, node11.node13 36.549, node11.node14 33.691, node11.node15 45.199, node11.node16 43.565 node11.node17 42.240, node11.node18 48.380, node11.node19 43.115, node11.node20 65.517, node11.node21 20.667 node11.node22 51.332, node11.node23 33.904, node11.node24 37.342, node11.node25 55.564, node12.node1 72.149 node12.node2 14.804, node12.node3 47.459, node12.node4 19.365, node12.node5 58.634, node12.node6 7.504 node12.node7 31.251, node12.node8 46.422, node12.node9 42.630, node12.node10 58.006, node12.node11 22.334 node12.node13 58.863, node12.node14 51.539, node12.node15 24.430, node12.node16 58.752, node12.node17 55.375 node12.node18 26.697, node12.node19 22.405, node12.node20 74.041, node12.node21 41.580, node12.node22 49.973 node12.node23 49.988, node12.node24 46.241, node12.node25 76.249, node13.node1 48.181, node13.node2 44.130 node13.node3 21.519, node13.node4 70.878, node13.node5 2.944, node13.node6 56.354, node13.node7 65.601 node13.node8 68.363, node13.node9 55.647, node13.node10 33.420, node13.node11 36.549, node13.node12 58.863 node13.node14 29.981, node13.node15 81.272, node13.node16 40.691, node13.node17 44.646, node13.node18 84.770 node13.node19 79.202, node13.node20 68.945, node13.node21 22.171, node13.node22 72.163, node13.node23 34.748 node13.node24 49.771, node13.node25 29.675, node14.node1 23.706, node14.node2 38.741, node14.node3 42.380 node14.node4 69.224, node14.node5 32.441, node14.node6 53.054, node14.node7 71.887, node14.node8 41.216 node14.node9 28.507, node14.node10 6.933, node14.node11 33.691, node14.node12 51.539, node14.node13 29.981 node14.node15 67.612, node14.node16 11.907, node14.node17 14.713, node14.node18 72.321, node14.node19 65.769 node14.node20 39.645, node14.node21 15.334, node14.node22 44.542, node14.node23 5.089, node14.node24 21.262 node14.node25 26.986, node15.node1 83.901, node15.node2 37.746, node15.node3 71.735, node15.node4 30.246 node15.node5 81.437, node15.node6 30.618, node15.node7 48.337, node15.node8 45.347, node15.node9 48.384 node15.node10 73.030, node15.node11 45.199, node15.node12 24.430, node15.node13 81.272, node15.node14 67.612 node15.node16 71.481, node15.node17 66.498, node15.node18 5.392, node15.node19 2.084, node15.node20 78.343 node15.node21 61.547, node15.node22 47.336, node15.node23 64.575, node15.node24 54.945, node15.node25 94.229 node16.node1 13.460, node16.node2 47.506, node16.node3 54.282, node16.node4 77.382, node16.node5 43.350 node16.node6 61.422, node16.node7 81.889, node16.node8 37.424, node16.node9 26.123, node16.node10 7.429 node16.node11 43.565, node16.node12 58.752, node16.node13 40.691, node16.node14 11.907, node16.node15 71.481 node16.node17 6.349, node16.node18 76.541, node16.node19 69.821, node16.node20 28.261, node16.node21 27.006 node16.node22 39.943, node16.node23 9.702, node16.node24 18.137, node16.node25 28.914, node17.node1 17.418 node17.node2 45.260, node17.node3 56.226, node17.node4 74.381, node17.node5 47.143, node17.node6 58.700 node17.node7 80.223, node17.node8 31.085, node17.node9 20.029, node17.node10 12.773, node17.node11 42.240 node17.node12 55.375, node17.node13 44.646, node17.node14 14.713, node17.node15 66.498, node17.node16 6.349 node17.node18 71.654, node17.node19 64.914, node17.node20 25.323, node17.node21 28.234, node17.node22 33.598 node17.node23 10.483, node17.node24 12.143, node17.node25 35.211, node18.node1 89.068, node18.node2 40.821 node18.node3 74.133, node18.node4 28.805, node18.node5 84.787, node18.node6 32.029, node18.node7 47.246 node18.node8 50.710, node18.node9 53.716, node18.node10 77.884, node18.node11 48.380, node18.node12 26.697 node18.node13 84.770, node18.node14 72.321, node18.node15 5.392, node18.node16 76.541, node18.node17 71.654 node18.node19 6.742, node18.node20 83.735, node18.node21 65.607, node18.node22 52.643, node18.node23 69.434 node18.node24 60.188, node18.node25 98.773, node19.node1 82.327, node19.node2 35.662, node19.node3 69.671 node19.node4 29.034, node19.node5 79.359, node19.node6 28.697, node19.node7 46.945, node19.node8 44.469 node19.node9 47.032, node19.node10 71.250, node19.node11 43.115, node19.node12 22.405, node19.node13 79.202 node19.node14 65.769, node19.node15 2.084, node19.node16 69.821, node19.node17 64.914, node19.node18 6.742 node19.node20 77.252, node19.node21 59.535, node19.node22 46.610, node19.node23 62.796, node19.node24 53.452 node19.node25 92.332, node20.node1 24.970, node20.node2 66.988, node20.node3 81.548, node20.node4 93.392 node20.node5 71.611, node20.node6 78.905, node20.node7 102.124, node20.node8 33.601, node20.node9 31.543 node20.node10 35.552, node20.node11 65.517, node20.node12 74.041, node20.node13 68.945, node20.node14 39.645 node20.node15 78.343, node20.node16 28.261, node20.node17 25.323, node20.node18 83.735, node20.node19 77.252 node20.node21 53.528, node20.node22 32.998, node20.node23 35.792, node20.node24 28.532, node20.node25 52.138 node21.node1 38.969, node21.node2 27.216, node21.node3 28.090, node21.node4 57.356, node21.node5 23.589 node21.node6 41.358, node21.node7 57.738, node21.node8 46.744, node21.node9 34.296, node21.node10 21.971 node21.node11 20.667, node21.node12 41.580, node21.node13 22.171, node21.node14 15.334, node21.node15 61.547 node21.node16 27.006, node21.node17 28.234, node21.node18 65.607, node21.node19 59.535, node21.node20 53.528 node21.node22 50.682, node21.node23 17.888, node21.node24 29.513, node21.node25 34.955, node22.node1 47.546 node22.node2 49.019, node22.node3 76.008, node22.node4 68.130, node22.node5 73.991, node22.node6 56.574 node22.node7 80.959, node22.node8 4.171, node22.node9 16.518, node22.node10 45.713, node22.node11 51.332 node22.node12 49.973, node22.node13 72.163, node22.node14 44.542, node22.node15 47.336, node22.node16 39.943 node22.node17 33.598, node22.node18 52.643, node22.node19 46.610, node22.node20 32.998, node22.node21 50.682 node22.node23 39.500, node22.node24 23.295, node22.node25 68.758, node23.node1 22.911, node23.node2 38.107 node23.node3 45.773, node23.node4 68.270, node23.node5 37.112, node23.node6 52.199, node23.node7 72.245 node23.node8 36.228, node23.node9 23.594, node23.node10 8.455, node23.node11 33.904, node23.node12 49.988 node23.node13 34.748, node23.node14 5.089, node23.node15 64.575, node23.node16 9.702, node23.node17 10.483 node23.node18 69.434, node23.node19 62.796, node23.node20 35.792, node23.node21 17.888, node23.node22 39.500 node23.node24 16.207, node23.node25 31.038, node24.node1 29.169, node24.node2 38.457, node24.node3 56.943 node24.node4 65.577, node24.node5 51.845, node24.node6 50.613, node24.node7 73.601, node24.node8 20.115 node24.node9 8.004, node24.node10 22.797, node24.node11 37.342, node24.node12 46.241, node24.node13 49.771 node24.node14 21.262, node24.node15 54.945, node24.node16 18.137, node24.node17 12.143, node24.node18 60.188 node24.node19 53.452, node24.node20 28.532, node24.node21 29.513, node24.node22 23.295, node24.node23 16.207 node24.node25 46.099, node25.node1 27.279, node25.node2 62.136, node25.node3 50.674, node25.node4 92.276 node25.node5 32.473, node25.node6 76.312, node25.node7 91.132, node25.node8 66.029, node25.node9 53.999 node25.node10 23.323, node25.node11 55.564, node25.node12 76.249, node25.node13 29.675, node25.node14 26.986 node25.node15 94.229, node25.node16 28.914, node25.node17 35.211, node25.node18 98.773, node25.node19 92.332 node25.node20 52.138, node25.node21 34.955, node25.node22 68.758, node25.node23 31.038, node25.node24 46.099
Arcs: data set 1
My first attempt to generate a sparse directed graph, resulted in a disconnected graph. Here is what I did:
An arc \(i \rightarrow j\) is selected with probability 0.5 if its length is less than 30. In GAMS, you could write this as:
set a1(i,j) ‘directed arcs v1’;a1(i,j)$ (ord(i)<>ord(j) and d(i,j)<35) = uniform(0,1)<0.4;
The goal of all this was to generate a “nice-looking” graph with short arcs and without self-loops.
Unfortunately, this approach will yield a disconnected graph. I.e., there is no path for all pairs of nodes \(s \rightarrow t\). Here \(s\) is the source node and \(t\) is the destination node. There are algorithms to find all strongly connected components (subsets of nodes that are connected) [1]. With this, we can see that my approach was inadequate to form a nice, connected graph.
---- 182 SET a1 directed arcs v1 node1 .node10, node1 .node24, node1 .node25, node2 .node3 , node2 .node11, node2 .node12, node3 .node2 node3 .node21, node4 .node6 , node4 .node15, node4 .node18, node4 .node19, node5 .node25, node6 .node11 node6 .node15, node7 .node4 , node8 .node9 , node9 .node10, node9 .node16, node9 .node17, node9 .node24 node10.node1 , node10.node14, node10.node23, node10.node25, node11.node2 , node11.node12, node11.node23 node12.node11, node13.node10, node13.node14, node13.node21, node14.node1 , node14.node13, node14.node21 node14.node23, node15.node6 , node15.node12, node15.node18, node15.node19, node16.node9 , node16.node10 node16.node14, node16.node23, node16.node25, node17.node8 , node17.node9 , node17.node24, node18.node4 node18.node15, node19.node12, node19.node15, node19.node18, node20.node16, node21.node14, node21.node24 node21.node25, node22.node8 , node22.node24, node23.node9 , node23.node14, node23.node17, node23.node21 node24.node8 , node24.node17, node24.node20, node24.node22, node25.node5 , node25.node10, node25.node23 ---- 182 SET icomp1 node/component mapping for arc set a1 comp1 comp2 comp3 comp4 comp5 node1 YES node2 YES node3 YES node4 YES node5 YES node6 YES node7 YES node8 YES node9 YES node10 YES node11 YES node12 YES node13 YES node14 YES node15 YES node16 YES node17 YES node18 YES node19 YES node20 YES node21 YES node22 YES node23 YES node24 YES node25 YES
Here is a picture:
 |
| Random arcs v1: disconnected components |
The light grey arrows represent arcs that have endpoints in different components.
As I really want a completely connected graph, there are some repair strategies we can employ:
- Try again with another random seed. Repeat until happy.
- Tinker with the parameters of the generation process (max length, sparseness).
- Use the strongly connected components results and repair by judiciously adding arcs.
When I use strategy 2, resulting in the following code:
set a2(i,j) ‘directed arcs v2’;a2(i,j)$ (ord(i)<>ord(j) and d(i,j)<40) = uniform(0,1)<0.5;
we get a strongly connected graph:
---- 182 SET a2 directed arcs v2 node1 .node14, node1 .node16, node1 .node17, node1 .node21, node1 .node24, node1 .node25, node2 .node3 node2 .node6 , node2 .node7 , node2 .node9 , node2 .node12, node2 .node14, node2 .node15, node2 .node21 node2 .node24, node3 .node11, node3 .node21, node4 .node2 , node4 .node7 , node4 .node12, node4 .node15 node5 .node11, node5 .node13, node5 .node23, node5 .node25, node6 .node11, node6 .node12, node6 .node18 node6 .node19, node7 .node2 , node7 .node6 , node8 .node22, node8 .node23, node8 .node24, node9 .node1 node9 .node10, node9 .node17, node9 .node21, node9 .node23, node9 .node24, node10.node5 , node10.node13 node10.node16, node10.node20, node10.node23, node10.node25, node11.node3 , node11.node4 , node11.node5 node11.node6 , node11.node9 , node11.node13, node11.node23, node11.node24, node12.node2 , node12.node6 node12.node19, node13.node3 , node13.node10, node13.node11, node13.node21, node14.node10, node14.node11 node14.node13, node14.node16, node15.node2 , node15.node4 , node15.node12, node15.node18, node15.node19 node16.node1 , node16.node8 , node16.node10, node16.node20, node16.node21, node16.node22, node16.node23 node17.node10, node17.node21, node18.node4 , node18.node12, node18.node15, node19.node2 , node19.node6 node19.node12, node20.node1 , node20.node8 , node20.node9 , node20.node17, node21.node1 , node21.node5 node21.node9 , node21.node11, node21.node13, node21.node17, node21.node23, node21.node25, node22.node8 node22.node9 , node22.node16, node22.node17, node23.node2 , node23.node10, node23.node11, node23.node16 node23.node17, node23.node21, node23.node24, node23.node25, node24.node2 , node24.node8 , node24.node11 node24.node14, node24.node20, node24.node21, node24.node22, node24.node23, node25.node1 , node25.node14 node25.node16 ---- 182 SET icomp2 node/component mapping for arc set a2 comp1 node1 YES node2 YES node3 YES node4 YES node5 YES node6 YES node7 YES node8 YES node9 YES node10 YES node11 YES node12 YES node13 YES node14 YES node15 YES node16 YES node17 YES node18 YES node19 YES node20 YES node21 YES node22 YES node23 YES node24 YES node25 YES
Instead of this trials-and-error approach, it is interesting to see if we can use a model to help us find sparse directed graphs that are connected.
The problem I want to put my teeth into here is:
- Given a set of \(n\) nodes, and a set of candidate (directed) arcs \(A\),
- try to find the smallest subset of arcs,
- such that the resulting graph is strongly connected.
This problem is related to finding a minimum spanning tree (MST), and we can borrow ideas from the flow formulations for that problem [2]. The difference lies in the fact that we are dealing with a sparse, directed graph, whereas the MST problem formulations operate on a complete, undirected graph. I want to mention that in the MST flow formulations, all directed arcs are essentially replaced by two directed arcs. So it is a bit closer to what we have here. The main issue is that we have sparsity: not all arcs exist.
Flow formulation 1
We can directly implement the idea that for any two different nodes \(s,t\) there should be a feasible path \(s \rightarrow t\). So we can do something like:
| Flow formulation 1 |
|---|
| \[\begin{align} \min& \sum_{(i\rightarrow j)\in A}\color{darkblue}c_{i,j}\cdot\color{darkred}u_{i,j} \ &\sum_{(j\rightarrow i)\in A} \color{darkred}f_{j,i,s,t} + \color{darkblue}{\mathit{supply}}_{i,s} = \sum_{(i\rightarrow j)\in A} \color{darkred}f_{i,j,s,t} + \color{darkblue}{\mathit{demand}}_{i,t} && \forall i,s,t|s\ne t \ & \color{darkred}u_{i,j}=0 \implies \color{darkred}f_{i,j,s,t}=0 \& \color{darkred}u_{i,j},\color{darkred}f_{i,j,s,t}\in \{0,1\} \ &\color{darkblue}{\mathit{supply}}_{i,s} = \begin{cases} 1 & \text{if $ i=s$ } \ 0 & \text{otherwise} \end{cases} \ &\color{darkblue}{\mathit{demand}}_{i,t} = \begin{cases} 1 & \text{if $ i=t$ } \ 0 & \text{otherwise} \end{cases}\end{align} \] |
- The first constraint is based on a standard flow balance or Kirchhoff equation: the total inflow of a node equals the total outflow. The complication is that we don’t have just a single flow \(i \rightarrow j\): \(\color{darkred}f_{i,j}\) but rather a whole bunch of them: \(\color{darkred}f_{i,j,s,t}\) is the flow along arc \(i \rightarrow j\) for the path \(s \rightarrow t\).
- The variable \(\color{darkred}u_{i,j} \in \{0,1\}\) keeps track of used arcs (a subset of \(A\)).
- The implication \(\color{darkred}u_{i,j}=0 \implies \color{darkred}f_{i,j,s,t}=0\) can be implemented as \[ \color{darkred}f_{i,j,s,t} \le \color{darkred}u_{i,j} \>\> \forall i\ne j,s\ne t\] This is the disaggregated version. We can aggregate aggressively: \[\sum_{s\ne t} \color{darkred}f_{i,j,s,t} \le (n^2-n)\color{darkred}u_{i,j}\>\>\forall i\ne j \] or we can do something in between like \[\sum_{s|s\ne t} \color{darkred}f_{i,j,s,t} \le (n-1)\color{darkred}u_{i,j}\>\>\forall i\ne j,t \]
- The parameters \(\color{darkblue}{\mathit{supply}}_{i,s}\) and \(\color{darkblue}{\mathit{demand}}_{i,t}\) are extremely sparse. This is exploited in GAMS.
- We can use \(\color{darkblue}c_{i,j}=1\) to minimize the number of used arcs, or \(\color{darkblue}c_{i,j}=\color{darkblue}d_{i,j}\) to make short arcs preferable to long arcs.
- For network problems like the shortest path problem, the solution is integer-valued automatically. Here, the network structure is destroyed by the \(\color{darkred}u\) variables. This would mean that we need to use binary flow variables. However, I think we can drop the integer restrictions on \(\color{darkred}f\), for two reasons. In practice, we may still observe integer flows (I have no proof that this is always the case; just an observation based on limited data). Secondly, even if the flow is fractional and split over different arcs, that is fine for the purpose of this model. We are only really interested in the \(\color{darkred}u\) variables. And these variables only worry about flow along an arc being zero or not. Minimizing the number of nonzero \(\color{darkred}u\) helps to prevent “damaging” fractional flow, i.e., flow that causes the objective to increase. Obviously, this reduces the number of discrete variables enormously. The performance is much better as a result.
Flow formulation 2
Here we use a flow formulation where we optimize in one swoop all flows from source \(s\) to all destinations \(t\ne s\). That means our flow variables only need one extra dimension: \(s\). So instead of \(\color{darkred}f_{i,j,s,t}\) we have \(\color{darkred}f_{i,j,s}\). The model looks like:
| Flow formulation 2 |
|---|
| \[\begin{align} \min& \sum_{(i\rightarrow j)\in A}\color{darkblue}c_{i,j}\cdot\color{darkred}u_{i,j} \ &\sum_{(j\rightarrow i)\in A} \color{darkred}f_{j,i,s} + \color{darkblue}{\mathit{supply}}_{i,s} = \sum_{(i\rightarrow j)\in A} \color{darkred}f_{i,j,s} + \color{darkblue}{\mathit{demand}}_{i,s} && \forall i,s \ & \color{darkred}u_{i,j}=0 \implies \color{darkred}f_{i,j,s}=0 \& \color{darkred}u_{i,j} \in \{0,1\},\color{darkred}f_{i,j,s}\in \{0,1,2,\dots\} \ &\color{darkblue}{\mathit{supply}}_{i,s} = \begin{cases} n-1 & \text{if $ i=s$ } \ 0 & \text{otherwise} \end{cases} \ &\color{darkblue}{\mathit{demand}}_{i,s} = \begin{cases} 1 & \text{if $ i\ne s$ } \ 0 & \text{if $ i=s$ } \end{cases}\end{align} \] |
- The flow variables are no longer binary. We must make them integers.
- Again, as in the previous formulation 1, I relax the flow variables to be continuous.
- The implication \(\color{darkred}u_{i,j}=0 \implies \color{darkred}f_{i,j,s}=0\) can again be implemented in different ways. The first one is simply: \[\color{darkred}f_{i,j,s} \le (n-1)\color{darkred}u_{i,j}\>\>\forall i,j,s|i\ne j\] The aggregated version would be: \[\sum_s \color{darkred}f_{i,j,s} \le n(n-1)\color{darkred}u_{i,j}\>\>\forall i\ne j\]
Results
I implemented both the disaggregated and fully aggregated versions of formulations 1 and 2.
When we use cost coefficients \(\color{darkred}c_{i,j}=1\) (i.e., minimize the number of arcs subject to connectivity constraints, starting with data set 2), we see:
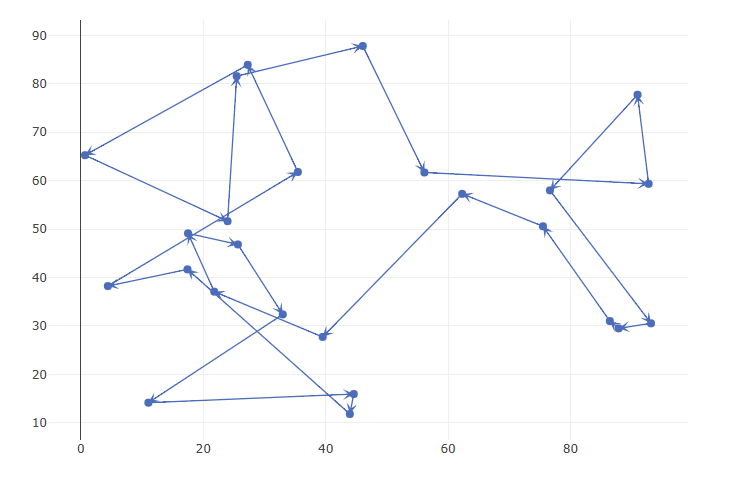 |
| Minimize number of arcs needed for connectivity (starting from data set 2) |
This looks like a TSP tour (most likely not the shortest). Indeed, when we minimize the number of arcs, while remaining connected, we can’t do better than a tour with \(n=25\) arcs.
The timings were:
---- 319 PARAMETER results model 1a model 1b model 2a model 2b Variables 72121.000 72121.000 3121.000 3121.000 Discrete 120.000 120.000 120.000 120.000 Equations 87001.000 15121.000 3626.000 746.000 Modelstat IntFeas Optimal Optimal Optimal Objective 27.000 25.000 25.000 25.000 Solver time 1000.494 551.264 5.303 5.317 Nodes 8.000 37.000 Gap% 8.000
The “a” models are the disaggregated versions, and the “b” ones are aggregated. A time limit of 1,000 seconds was used. We see model 1a hits this time limit.
If we use \(\color{darkblue}c_{i,j}=\color{darkred}d_{i,j}\) (i.e., penalize long arcs), we get different solution times:
---- 319 PARAMETER results model 1a model 1b model 2a model 2b Variables 72121.000 72121.000 3121.000 3121.000 Discrete 120.000 120.000 120.000 120.000 Equations 87001.000 15121.000 3626.000 746.000 Modelstat Optimal Optimal Optimal IntFeas Objective 487.546 487.546 487.546 487.546 Solver time 14.910 479.898 2.177 4.471 Nodes 7.000 15.000 102.000
Model 2b is declared integer feasible as it hits the default gap tolerance (1.0e-4) before proving optimality. My intuition about why this objective is faster: we make it easier for the solver to distinguish between solutions. With \(\color{darkblue}c_{i,j}=1\) many solutions have the same objective while with \(\color{darkblue}c_{i,j}=\color{darkred}d_{i,j}\) different solutions are likely to have a different objective function value. More distinction.
 |
| Using lengths as cost coefficients gives a slightly different tour. |
Of course, we can change the objective to handle something like:
- try to stay as close to \(2n\) arcs as possible (deviate with high cost)
- minimize the number arcs or sum of weighted arcs (with lower cost)
This can give a picture like:
Formulating strong connectivity as (linear) constraints is an interesting modeling exercise.
Some other related problems that are possibly more difficult to tackle:
- Using the disconnected graph from data set 1, use the minimum number of additional arcs to make the graph strongly connected.
- Use a mixed-integer formulation to form the strongly connected components (like Tarjan’s algorithm).
GAMS Model
$ onText
1. Generate random x,y coordates for nodes and calculate
their distances
2. Form 2 arc sets
data set 1: not enough to form a strongly connected graph
data set 2: with more arcs, we have a connected graph
3. Use Tarjan’s algorithm to find strongly connected components.
4. Form MIP models to remove arcs from data set 2 so that a
connected graph remains.
formulation 1: add s,t (source,destination) indices to flow variables
formulation 2: all destonation path approach
this means we only need to add an s (source) index
5. MIP model: find a connected graph with 2*n arcs
6. Visualization using plotly JS
$ offText
$ set numNodes 25
option seed=1234, reslim=1000;
*——————————————————-
* 1. nodes
*——————————————————-
sets
i ‘nodes’ /node1*node%numNodes%/
c ‘coordinates’ /x,y/
;
alias (i,j);
parameters
p(i,c) ‘node locations (points)’
d(i,j) ‘distances’
;
p(i,c) = uniform(0,100);
d(i,j) = sqrt(sum(c,sqr(p(i,c)-p(j,c))));
option d:3:0:7;
display i,p,d;
*——————————————————-
* arcs
*——————————————————-
sets
offd(i,j) ‘off-diagonal: no self-loops’
a1(i,j) ‘directed arcs v1’
a2(i,j) ‘directed arcs v2’
;
* generate a sparse graph
offd(i,j) = ord(i)<>ord(j);
a1(offd)$ (d(offd)<35) = uniform(0,1)<0.4;
a2(offd)$ (d(offd)<40) = uniform(0,1)<0.5;
option a1:0:0:7,a2:0:0:7;
*——————————————————-
* strongly connected components (SCCs)
*——————————————————-
$ ontext
This will show:
Data set: i,a1 -> icomp1
Number of strongly connected components:3
Data set: i,a2 -> icomp2
Number of strongly connected components:1
$ offtext
sets
comp ‘strongly connected components (superset)’ /comp1*comp100/
icomp1(i,comp) ‘node/component mapping for arc set a1’
icomp2(i,comp) ‘node/component mapping for arc set a2’
;
EmbeddedCode Python:
#——————————————————————————
# import nodes and arcs from GAMS
#——————————————————————————
# https://youcademy.org/tarjans-scc-algorithm/
def dfs(graph, node, counter, index, low_link, stack, on_stack, sccs):
“””
Perform Depth-First Search (DFS) to find Strongly Connected Components (SCCs)
Args:
graph: Adjacency list representation of the graph
node: Current node being processed
counter: Counter for assigning discovery indices
index: Mapping of node to its index in the DFS
low_link: Mapping of node to its low-link value
stack: Stack to keep track of nodes in the DFS search tree
on_stack: Set of nodes currently on the stack
sccs: List to store the found Strongly Connected Components
“””
index[node] = counter
low_link[node] = counter
counter += 1
stack.append(node)
on_stack.add(node)
# Iterate over all neighbors of the current node
for neighbor in graph[node]:
if neighbor not in index:
# If the neighbor hasn’t been visited, perfom dfs on it’s subtree
dfs(graph, neighbor, counter, index, low_link, stack, on_stack, sccs)
# Update the low-link value based on the neighbor’s low-link
low_link[node] = min(low_link[node], low_link[neighbor])
elif neighbor in on_stack:
low_link[node] = min(low_link[node], index[neighbor])
# Check if the current node is a root node for an SCC
if low_link[node] == index[node]:
scc = []
# Pop all nodes from the stack upto
# the root node and add them to current SCC
while stack:
top = stack.pop()
on_stack.remove(top)
scc.append(top)
if top == node:
break
sccs.append(scc)
def tarjan_scc(graph):
“””
Find the Strongly Connected Components (SCCs) in the given graph using Tarjan’s algorithm.
Args:
graph: Adjacency list representation of the graph
Returns:
list: List of Strongly Connected Components (SCCs)
“””
counter = 0 # Counter to set discovery indices
index = {} # Map to store discovery index of each node
low_link = {} # Map to store low-link value of each node
stack = [] # Stack to store nodes which yet to be mapped to an SCC
on_stack = set() # Set to store nodes which are present on stack
sccs = [] # List to store all SCCs in the given graph
for node in graph:
if node not in index:
# Current node is not visited yet
# So let’s perform a DFS and group nodes into SCC’s
dfs(graph, node, counter, index, low_link, stack, on_stack, sccs)
return sccs
def loadDataFromGAMS(nodeset,arcset):
# set up graph in format required by tarjan routine
# dictionary with {node:list_of_nodes} where
# list containts nodes pointed to by node
graph = {node:[] for node in gams.get(nodeset)}
for a in gams.get(arcset):
graph[a[0]].append(a[1])
return(graph)
def saveResultsToGAMS(sccs,icompset):
# GAMS set is defined over (node,comp)
icomp = []
for comp,arr in enumerate(sccs):
scomp = f”comp{comp+1}”
for node in arr:
icomp.append((node,scomp))
gams.set(icompset,icomp)
def run(nodeset,arcset,icompset):
gams.printLog(f”Data set: {nodeset},{arcset} -> {icompset}”)
graph = loadDataFromGAMS(nodeset,arcset)
sccs = tarjan_scc(graph)
gams.printLog(f”Number of strongly connected components:{len(sccs)}”)
saveResultsToGAMS(sccs,icompset)
run(“i”,”a1″,”icomp1″)
run(“i”,”a2″,”icomp2″)
endEmbeddedCode icomp1,icomp2
parameter ncomp(*) ‘number of disconnected components’;
option ncomp:0;
ncomp(“a1”) = sum(comp$ sum(icomp1(i,comp),1),1);
ncomp(“a2”) = sum(comp$ sum(icomp2(i,comp),1),1);
display a1,icomp1,a2,icomp2;
*——————————————————-
* reporting macros
*——————————————————-
parameter results(*,*);
acronym Optimal,IntFeas;
$ macro collect_stats(id,m) \
results(‘Variables’,id) = m.numvar; \
results(‘ Discrete’,id) = m.numdvar; \
results(‘Equations’,id) = m.numequ; \
results(‘Modelstat’,id) = m.modelstat; \
results(‘Modelstat’,id)$ (m.modelstat=1) = Optimal; \
results(‘Modelstat’,id)$ (m.modelstat=8) = IntFeas; \
results(‘Objective’,id) = m.objval; \
results(‘Solver time’,id) = m.etSolver; \
results(‘Nodes’,id) = m.nodusd; \
results(‘Gap%’,id)$ (m.solvestat=3) = 100*abs(m.objest – m.objval)/abs(m.objest); \
display results;
*——————————————————-
* flow model 1
* data set a2
*——————————————————-
* we need to add a source and destination index
alias(i,s,t);
set
a(i,j) ‘arcs’
;
parameter
supply1(i,s) ‘supply at supply nodes’
demand1(i,t) ‘demand at demand nodes’
M1 ‘big M’
cost(i,j) ‘cost coefficients’
;
supply1(s,s) = 1;
demand1(t,t) = 1;
M1 = sqr(card(i))-card(i);
binary variables
f1(i,j,s,t) ‘flow i → j on path s → t’
u(i,j) ‘arc is used’
;
variable z;
equations
nodebal1(i,s,t) ‘node balance’
usage1a(i,j,s,t) ‘usage of arc (disaggregated version)’
usage1b(i,j) ‘usage of arc (aggregated version)’
obj1 ‘objective’
;
nodebal1(i,s,t)$ offd(s,t)..
sum(a(j,i),f1(a,s,t)) + supply1(i,s) =e=
sum(a(i,j),f1(a,s,t)) + demand1(i,t);
* u(i,j) = 0 => f1(i,j,src,dst) = 0
* two versions (aggregated and disaggregated)
usage1a(a(i,j),s,t)$ offd(s,t).. f1(i,j,s,t) =l= u(i,j);
usage1b(a(i,j)).. sum(offd(s,t),f1(i,j,s,t)) =l= M1*u(i,j);
obj1.. z =e= sum(a,cost(a)*u(a));
model flowmodel1a /nodebal1,usage1a,obj1/;
model flowmodel1b /nodebal1,usage1b,obj1/;
*——————————————————-
* flow model 2
*——————————————————-
parameter
supply2(i,s) ‘supply at supply nodes’
demand2(i,s) ‘demand at demand nodes’
;
supply2(s,s) = card(i)-1;
demand2(offd(i,s)) = 1;
integer variables f2(i,j,s) ‘flow i → j on path from s’;
equations
nodebal2(i,s) ‘node balance’
usage2a(i,j,s) ‘usage of arc (disaggregated version)’
usage2b(i,j) ‘usage of arc (aggregated version)’
obj2 ‘objective’
;
nodebal2(i,s)..
sum(a(j,i),f2(a,s)) + supply2(i,s) =e=
sum(a(i,j),f2(a,s)) + demand2(i,s);
* use(i,j) = 0 => flow2(i,j,src) = 0
* again: two versions
usage2a(a(i,j),s).. f2(a,s) =l= card(i)*u(a);
usage2b(a).. sum(s,f2(a,s)) =l= M1*u(a);
model flowmodel2a /nodebal2,usage2a,obj1/;
model flowmodel2b /nodebal2,usage2b,obj1/;
*——————————————————-
* flow model 2 but with a given number of arcs as target
*——————————————————-
scalar numArcsUsed ‘target number of arcs’;
numArcsUsed = card(i)*2;
* deviations from target
positive variable d1,d2;
equation fixNumArcs ‘stay close to target number of arcs’;
fixNumArcs.. sum(a,u(a)) =e= numArcsUsed + d1 – d2;
equation obj2 ‘weighted multiple objective’;
* most emphasis on target number of arcs
obj2.. z =e= sum(a,cost(a)*u(a)) + 1e4*(d1+d2);
model flowmodel2afx /nodebal2,usage2a,obj2,fixNumArcs/;
*——————————————————-
* Solve models
*——————————————————-
* use the second data set
a(i,j) = a2(i,j);
* choose min number of arcs or weight by length
* the latter will prefer shorter arcs which may be
* giving better look graphs.
*cost(a) = 1;
cost(a) = d(a);
* relax the flow variables
f1.prior(i,j,s,t) = INF;
f2.prior(i,j,s) = INF;
solve flowmodel1a using mip minimizing z;
collect_stats(‘model 1a’,flowmodel1a)
solve flowmodel1b using mip minimizing z;
collect_stats(‘model 1b’,flowmodel1b)
solve flowmodel2a using mip minimizing z;
collect_stats(‘model 2a’,flowmodel2a)
solve flowmodel2b using mip minimizing z;
collect_stats(‘model 2b’,flowmodel2b)
solve flowmodel2afx using mip minimizing z;
collect_stats(‘model 2afx’,flowmodel2afx)
parameter usol(i,j) ‘solution of last solve’;
usol(a) = round(u.l(a));
*——————————————————-
* visualization
*——————————————————-
$ set htmlfile report.html
file html /%htmlfile%/
put html;
$ onPutS
<html>
<script id=”MathJax-script” async src=”https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js”></script>
<script src=”https://cdn.plot.ly/plotly-3.0.1.min.js” charset=”utf-8″></script>
<style>
table,th, td {
border: 1px solid black;
border-collapse: collapse;
padding-left: 10px;
padding-right: 10px;
}
p { max-width:800px; }
</style>
<script>
$ offPut
* export GAMS data to JS
* nodes
alias (comp,comp1,comp2);
put “nodes=[“/;
loop((icomp1(i,comp1),icomp2(i,comp2)),
put “{x:”,p(i,‘x’):0:3,“,y:”,p(i,‘y’):0:3,“,comp1:”,ord(comp1):0:0,“,comp2:”,ord(comp2):0:0,“},”/;
);
put “];”/;
* arc set 1
put “arcs1=[“/;
loop(a1(i,j),
put “{i:”,ord(i):0:0,“,j:”,ord(j):0:0,“},”/;
);
put “];”/;
* arc set 2
put “arcs2=[“/;
loop(a2(i,j),
put “{i:”,ord(i):0:0,“,j:”,ord(j):0:0,“},”/;
);
put “];”/;
put “ncomp1=”,ncomp(‘a1’):0:0,“;”/;
put “ncomp2=”,ncomp(‘a2’):0:0,“;”/;
* MIP solution
put “sol=[“/;
loop((i,j)$ usol(i,j),
put “{i:”,ord(i):0:0,“,j:”,ord(j):0:0,“},”/;
);
put “];”/;
$ onPut
// extract coordinates as arrays
xpoints = nodes.map(({x})=>x);
ypoints = nodes.map(({y})=>y);
n = nodes.length;
na1 = arcs1.length;
na2 = arcs1.length;
// color array
colors = [
‘#1f77b4’, // muted blue
‘#ff7f0e’, // safety orange
‘#2ca02c’, // cooked asparagus green
‘#d62728’, // brick red
‘#9467bd’, // muted purple
‘#8c564b’, // chestnut brown
‘#e377c2’, // raspberry yogurt pink
‘#7f7f7f’, // middle gray
‘#bcbd22’, // curry yellow-green
‘#17becf’ // blue-teal
];
function formColorArray(comp) {
scolor = [];
for (i=0; i<n; ++i) {
c = nodes[i][comp]-1;
scolor.push(colors[c % colors.length]);
}
return scolor;
}
scol1 = formColorArray(“comp1”);
scol2 = formColorArray(“comp2”);
// plotly trace for node plot
trace1 = {
x: xpoints,
y: ypoints,
mode: ‘markers’,
type: ‘scatter’,
marker: { color: ‘black’ }
};
// plotly trace for component plot
trace2 = {
x: xpoints,
y: ypoints,
mode: ‘markers’,
type: ‘scatter’,
marker: { color:scol1, size:8 }
};
trace3 = {
x: xpoints,
y: ypoints,
mode: ‘markers’,
type: ‘scatter’,
marker: { color:scol2, size:8 }
};
// annotations are used to plot arrows
function formAnnotations(arcs,comp,scolor) {
annots = []; // array with annotations
for (k=0; k < arcs.length; ++k) {
// (i,j) are node numbers (zero based)
i = arcs[k][‘i’]-1;
j = arcs[k][‘j’]-1;
// colors are component numbers (zero based)
ci = scolor[i];
cj = scolor[j];
// if different then use a light gray arrow
if (ci===cj) {
col = ci;
}
else {
col = ‘LightGray’;
}
// populate annotation
ann = {
ax:xpoints[i], ay:ypoints[i],
x:xpoints[j], y:ypoints[j],
axref:”x”, ayref:”y”,
xref:”x”, yref:”y”,
text:”, // if you want only the arrow
showarrow:true,
arrowhead:3,
arrowsize:1.4,
arrowwidth:1.3,
arrowcolor:col,
}
annots.push(ann);
}
return annots;
}
var layout2 = {showlegend: false, annotations:formAnnotations(arcs1,”comp1″,scol1) };
var layout3 = {showlegend: false, annotations:formAnnotations(arcs2,”comp2″,scol2) };
var layout4 = {showlegend: false, annotations:formAnnotations(sol,”comp2″,scol2) };
</script>
<body>
<h1>Generating Connected Graphs</h1>
<h2>Nodes</h2>
<p>The locations of the \(n=%numnodes%\) points are randomly generated and drawn from the uniform distribution.</p>
<div id=”myPlot1″ style=”width:100%;max-width:800px;height:600px”></div>
<script>Plotly.newPlot(‘myPlot1’, [trace1]);</script>
<h2>Arcs</h2>
<h3>Data set 1</h3>
We used simple GAMS code to generate <script>document.write(na1)</script>
arcs. The number of disconnected components is <script>document.write(ncomp1)</script>.
<div id=”myPlot2″ style=”width:100%;max-width:800px;height:600px”></div>
<script>Plotly.newPlot(‘myPlot2’, [trace2], layout2);</script>
<h3>Data set 2</h3>
This data set is yielding a strongly connected graph.
<div id=”myPlot3″ style=”width:100%;max-width:800px;height:600px”></div>
<script>Plotly.newPlot(‘myPlot3’, [trace3], layout3);</script>
<h3>MIP model results</h3>
<div id=”myPlot4″ style=”width:100%;max-width:800px;height:600px”></div>
<script>Plotly.newPlot(‘myPlot4’, [trace3], layout4);</script>
</body>
</html>
$ offPut
executetool ‘win32.ShellExecute “%htmlfile%“‘;
References
- Tarjan’s strongly connected components algorithm, https://en.wikipedia.org/wiki/Tarjan%27s_strongly_connected_components_algorithm
- Minimum Spanning Trees in Math Programming Models, https://yetanothermathprogrammingconsultant.blogspot.com/2021/03/minimum-spanning-trees-in-math.html


